4 minutes
LLM Quantization in Production
You’ve just trained or downloaded a large language model, and now comes the challenging part: deploying it efficiently in production. One term you’ll encounter frequently is “quantization” - a technique that can dramatically reduce your deployment costs and resource requirements. Let’s break down what this means for your team and how to make practical decisions about it.
What is Quantization and Why Should We Care?
Think of quantization as compression for your AI model. Just as you might compress a video file to stream it more efficiently, quantization compresses your model to run it more efficiently. Here are the immediate benefits:
- 💾 Reduced storage requirements (up to 75% smaller)
- 💰 Potentially lower infrastructure costs (30-60% in practice)
- ⚡ Faster inference times
- 🌱 Reduced energy consumption
Understanding the Tradeoffs
Rather than diving into complex math, let’s visualize what happens when you quantize a model. Here’s a simple demonstration that shows how quantization affects model weights:
# Simple quantization demo - see how weights change with different bit depths
...
def generate_signal(self, num_points: int = 1000) -> Tuple[np.ndarray, np.ndarray]:
"""Generate a sample distribution similar to LLM weights."""
t = np.linspace(0, 1, num_points)
# Create a primarily Gaussian distribution with some outliers
np.random.seed(42) # For reproducibility
# convert to FP16 to simulate real model weights
signal = np.random.normal(0, 0.3, num_points).astype(np.float16) # Main weight distribution
# Add some sparse outliers to mimic important weights
outlier_idx = np.random.choice(num_points, size=int(num_points * 0.05), replace=False)
signal[outlier_idx] += np.random.normal(0, 0.8, len(outlier_idx))
return t, signal
def quantize(self, signal: np.ndarray) -> np.ndarray:
"""Quantize the input signal to specified bit depth."""
# Scale signal to [0, 1]
normalized = (signal - np.min(signal)) / (np.max(signal) - np.min(signal))
# Quantize to discrete levels
quantized = np.round(normalized * (self.levels - 1)) / (self.levels - 1)
# Scale back to original range
return quantized * (np.max(signal) - np.min(signal)) + np.min(signal)
...
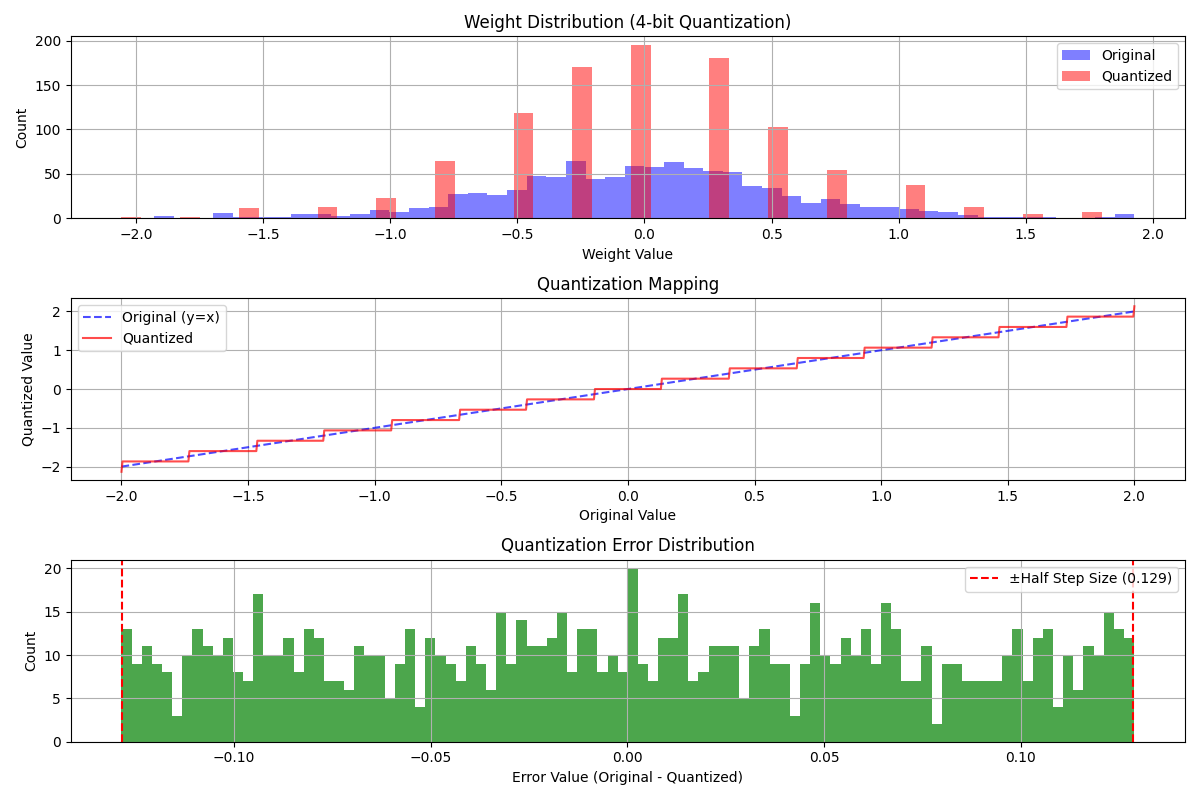
Understanding the Visualization
This demo shows the process of quantizing from FP16 (16-bit floating point) to lower precisions, simulating real-world LLM quantization. The visualization includes three graphs that help understand what happens during this process:
-
Weight Distribution (Top Graph)
- Blue shows original model weights - notice the bell curve shape with some outliers
- Red shows quantized weights - see how they cluster into distinct levels
- This clustering is what saves memory, but also shows what precision you’re giving up
-
Quantization Mapping (Middle Graph)
- Shows exactly how original values are mapped to their quantized versions
- Blue dashed line: y=x line (what values would be without quantization)
- Red line: Actual quantized values showing clear “staircase” pattern
- Each “step” in the red line is a valid quantization level
- The vertical jumps between steps are where rounding occurs The uniform step size shows how we’re using evenly-spaced quantization levels
-
Error Distribution (Bottom Graph)
- X-axis: Error = Original Value - Quantized Value
- Negative means we rounded up
- Positive means we rounded down
- Zero means perfect match
- Y-axis: Number of weights with each error value
- Values get rounded to the nearest quantization level
- The error is the distance to that nearest level
- With uniform spacing between levels, we get uniform distribution of errors
- This histogram helps us see if errors are biased in one direction
- X-axis: Error = Original Value - Quantized Value
These visualizations can help us make decisions about:
- Whether to use 8-bit vs 4-bit quantization
- Which model layers might need higher precision
- What kind of accuracy impact to expect
Quick Tip: Run this visualization on a sample of your model’s weights before full deployment. If you see large errors or severely distorted distributions, you might want to consider less aggressive quantization or mixed-precision approaches.
Practical Decision Guide for When to Use Different Quantization Levels
32-bit (No Quantization)
- During training
- When maximum accuracy is required
- When you have unlimited resources
16-bit
- Safe default for most deployments
- Minimal impact on model quality
- ~50% size reduction
- Supported by most hardware
8-bit
- Popular compromise
- ~75% size reduction
- Minor accuracy impact
- Great for cost optimization
- Well-supported by modern frameworks
4-bit
- Aggressive optimization
- ~87.5% size reduction
- Noticeable quality impact
- Requires careful testing
- Limited framework support
Cost Impact Analysis
Understanding the true cost impact of quantization requires looking at several factors. Here’s a breakdown:
| Model Size | Original (FP16) | 8-bit | 4-bit | Memory Impact |
|---|---|---|---|---|
| 7B params | 14GB | ~7GB | ~3.5GB | 50-75% reduction |
| 13B params | 26GB | ~13GB | ~6.5GB | 50-75% reduction |
| 70B params | 140GB | ~70GB | ~35GB | 50-75% reduction |
Cost Impact Varies By Usage:
- GPU Memory: 50-75% reduction in memory requirements
- Inference Speed: 1.5-3x speedup possible
- Throughput: Can often serve 2-3x more requests per GPU
- Total Cost Impact: 30-60% reduction in practice*
*Real cost savings depend on:
- Batch size optimization
- Framework overhead
- Hardware utilization
- Cooling and operational costs